数学 三 平方 の 定理 933321-三平方の定理 計算 30 60

中3数学 三平方の定理11 折り返した図形 すべて無料 星組の中学数学講座
三角形の角の反対側にある辺を対辺と言います。 そして 特に直角の対辺を斜辺を言います。 また、当然ですが、三角なので辺は3つあります。 三平方の定理とは、 『斜辺の2乗が、その他の辺の2乗の和に等しくなる』 というものです。三 平方 の 定理。 数学切り抜き帳 三平方の定理(ピタゴラスの定理)と公式の証明忍者が用いた三角の知恵|アタリマエ! 🤩 PDF from the original on Indeed, the foursquare theorem was proved earlier, in 1770 この関係を 三平方の定理 または ピタゴラスの定理 と言う。 三平方の定
三平方の定理 計算 30 60
三平方の定理 計算 30 60- S S が三角形のとき,さきほどの四平方の定理と一致するので,この定理はさきほどの定理の一般化になっています。 正射影と面積 上記の定理を証明するためには前提知識が二つ必要になります。 前提知識1 「平面 P P に含まれ,面積が S S である図形」を平面 Q Q に正射影したときの面積は S\cos\theta S cosθ である。 ただし, \theta θ は平面 P P と平面 Q Q のなす角。 これは有三平方の定理とは 三平方の定理(基本問題1) 例題と練習 三平方の定理(基本問題2) 例題と練習 三平方の定理(四角形の対角線) 例題と練習 特別な三角形 例題と練習 特別な三角形2 例題と練習 二等辺三角形の面積 例題と練習 三辺から三角形の面積を求める 例題と練習 座標上の2点間の距離 例題と
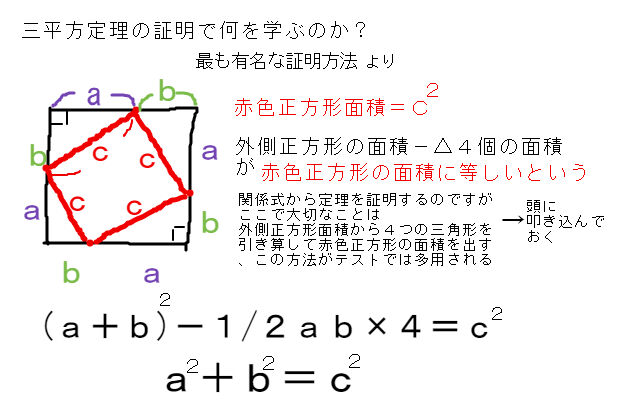
三平方定理の証明内容で最も覚えておくべきこと 中学 数学 理科の復習サイト
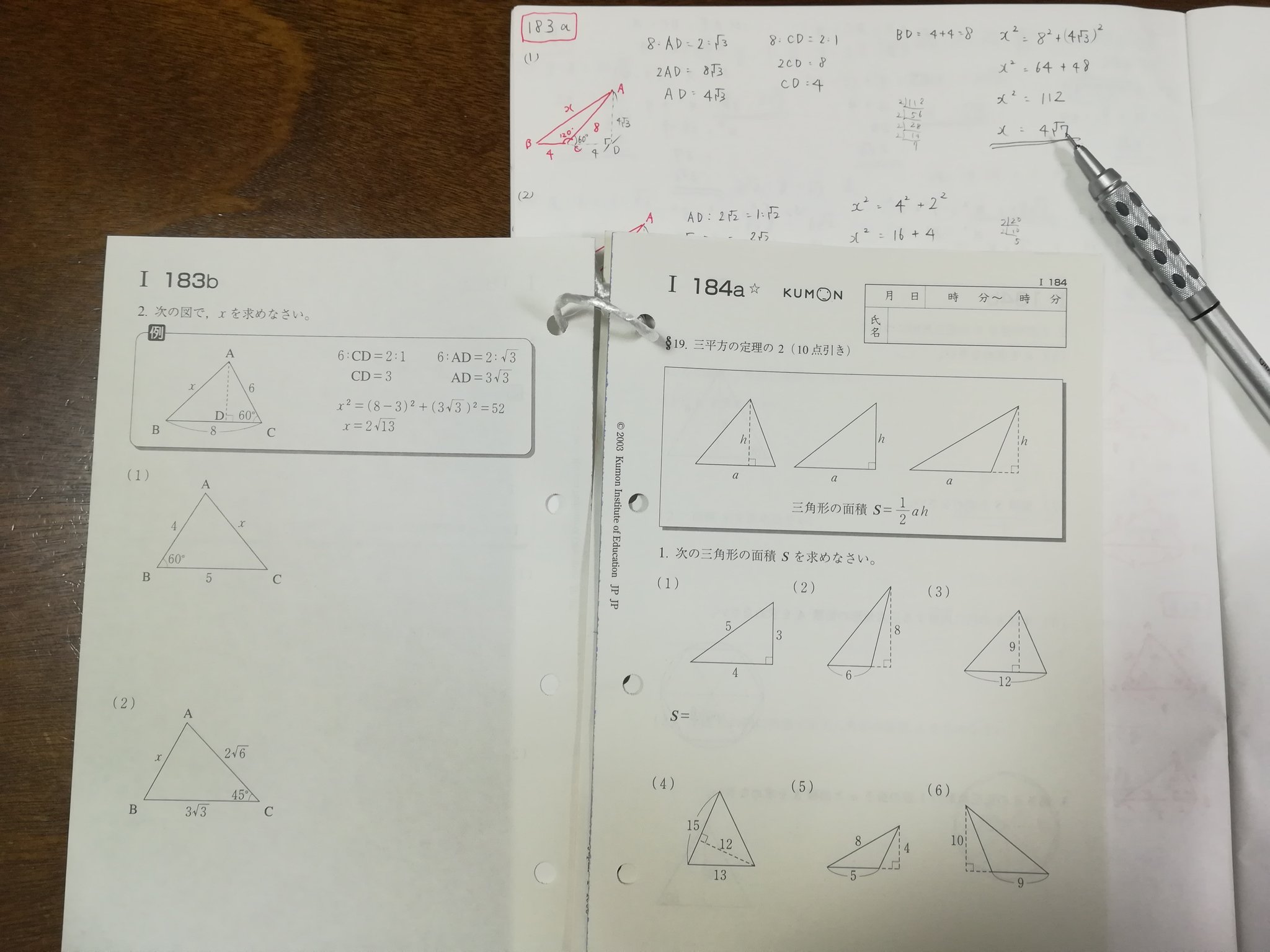
三平方の定理を使って面積を求める方法は? 問題を使って解説するよ! 次の三角形の面積を求めましょう。 まず、底辺を6㎝とした場合の高さとなるような線を引きます。 すると、三角形が2つの直角三角形に分けることができますね。 そこから左にあとは、三平方の定理で解決します。 ここで、計算を簡単にするために、 y = 1 y = 1 のときの相似な三角形で長さを求めましょう。 三角形 AEH A E H に三平方の定理を使うと、 AE = √10 A E = 10 なので、 これは、本来の図と相似比が 8 √10 8 10 です。 三角形動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru取材や仕事等の
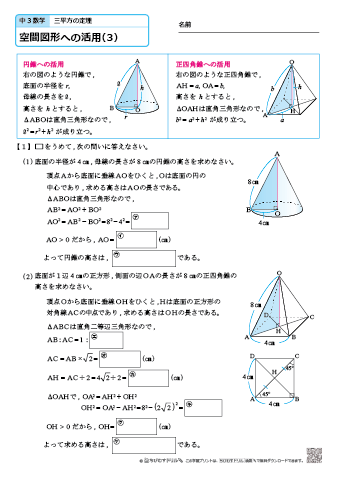
三平方の定理とは 三平方の定理(基本問題1) 例題と練習 三平方の定理(基本問題2) 例題と練習 三平方の定理(四角形の対角線) 例題と練習 特別な三角形 例題と練習 特別な三角形2 例題と練習 二等辺三角形の面積 例題と練習 三辺から三角形の面積を求める 例題と練習 座標上の2点間の距離 例題と数学b2 班 今井 亨 定道 勇斗 谷口 昂平 西川 太朗 二次元での定理を三次元に拡張 私たちはこの定理を三次元(立体)に拡張したときにどうなるのかというのに興味を持ち ました。そして、研究したところ三次元でも同じような定理が成り立つことがわかりまし た。だからほかにも三次元に解説 答え: 5 2 √ 7 5 2 7 (㎝) ~ポイント~ 三平方の定理を使う、このパターンは頻出なので 基本の型 として慣れておきましょう。 また、解説中に『ふつうに解く』と『工夫して解く』の2種類の解き方が登場していますので、確認しておいてください。 三平方の定理を利用して長方形の対角線を求める問題 この長方形の対角線の長さを求めよ。 ただしこの
三平方の定理 計算 30 60のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |
三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 | 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |
 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |
 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |
 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |
 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 | 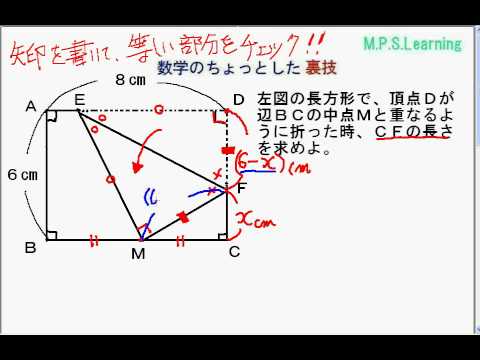 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |
 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 | 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |
 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |
三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |
 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |
 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |
 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |
 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 | 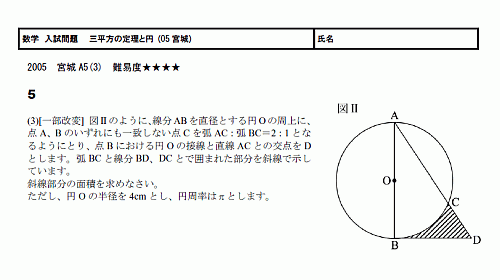 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 | 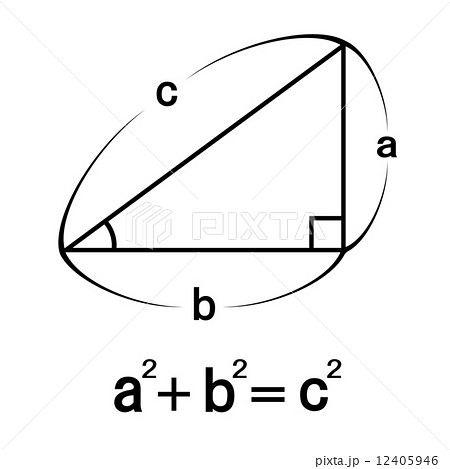 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |
 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |
 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |
 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 | 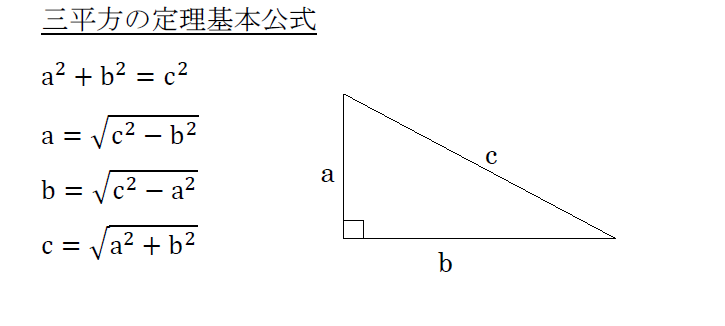 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |
 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 | 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |
三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |
 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 | 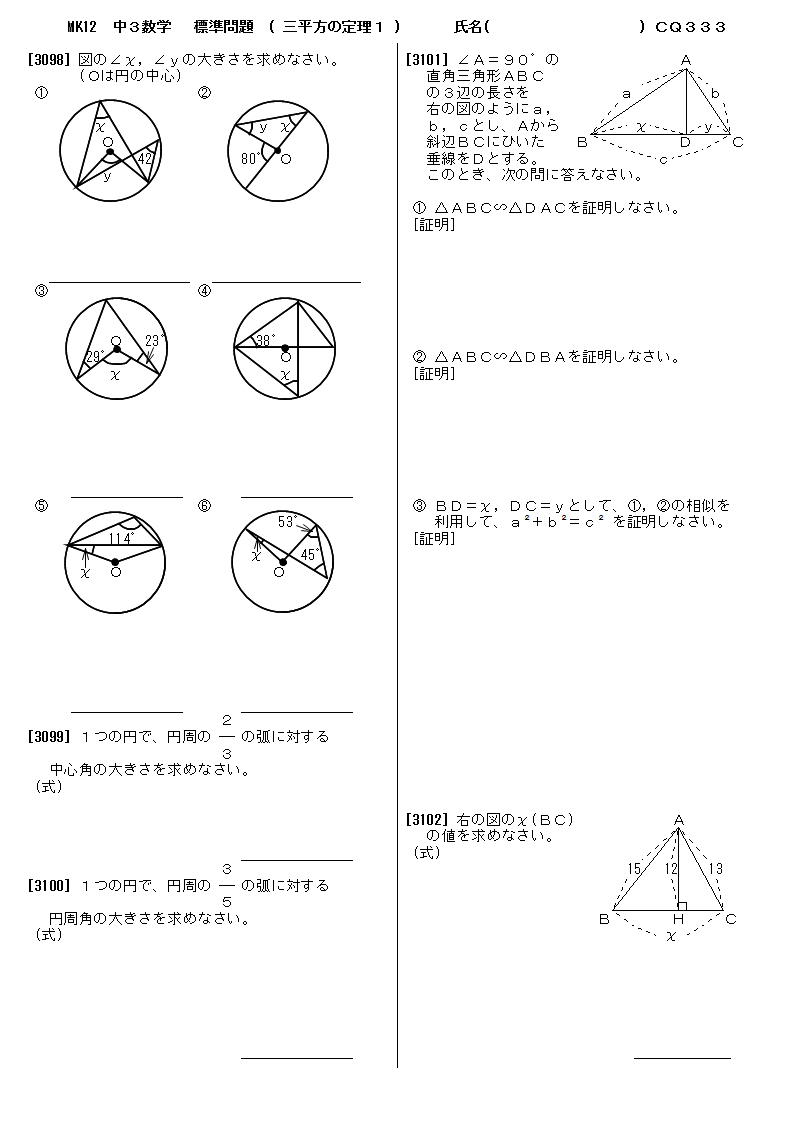 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |
 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |
三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 | 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |
 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 | 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |
 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 | 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |
 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 | 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |
 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 | 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |
 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |
 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |
 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |
 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |
 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |
 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |
 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 | 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |
 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 | 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |
 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |  三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |
 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 | 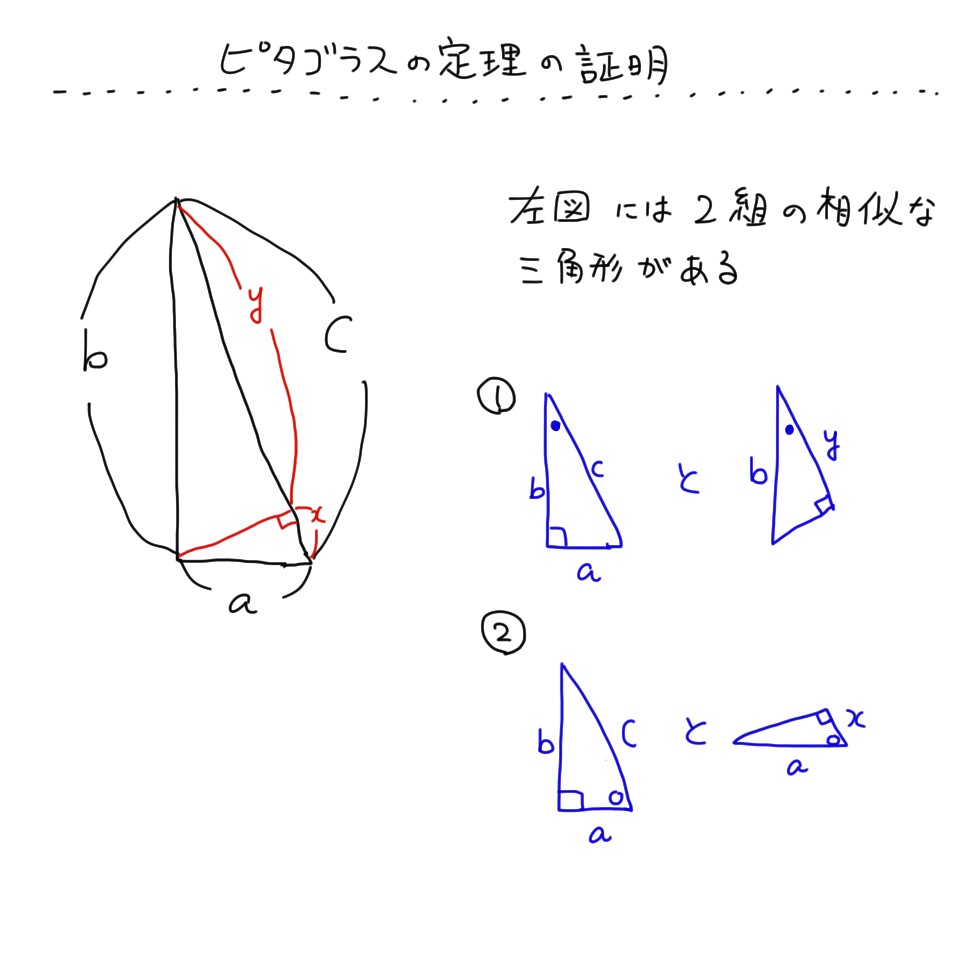 三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張 |
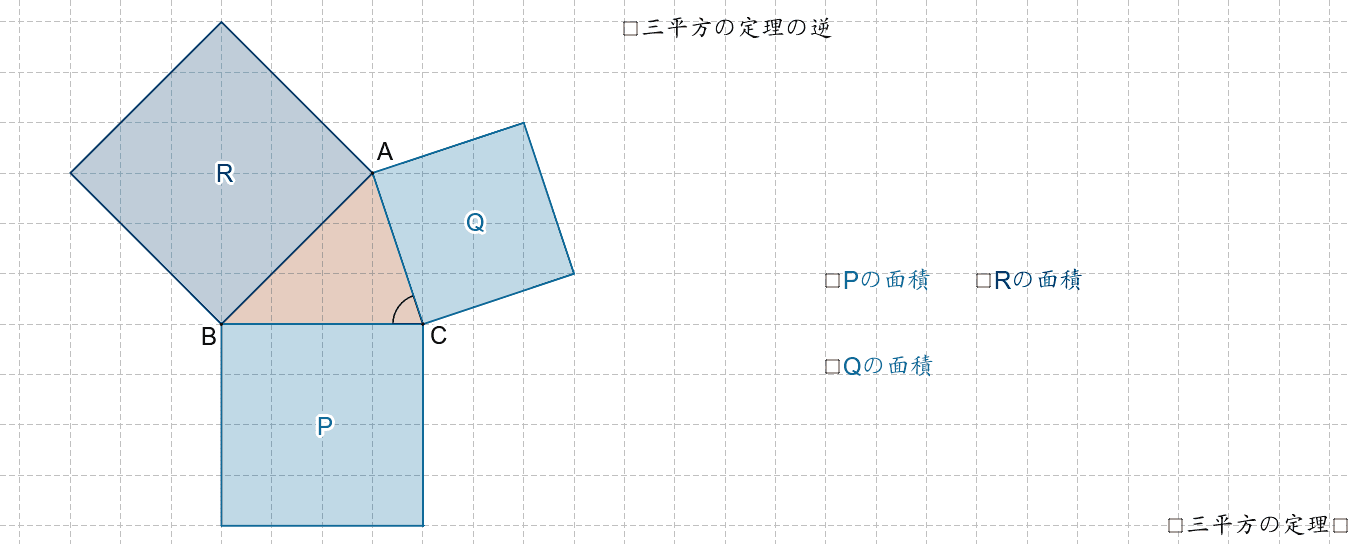
直角三角形の辺の長さを a、b、c (斜辺) とすると、a2+b2=c2 の関係になっています。この関係を三平方の定理といいます。*ピタゴラスの定理ともいいます。直角三角形において、斜辺(1番長い辺)の2乗は、残りの2辺のそれぞれの2乗の和に等しい証明のやり方三平方の定理の証おさらいとして三平方の定理は以下の通り。 これに対して、逆も成り立ちます。 三角形の各辺に関して、 c2 = a2 b2 c 2 = a 2 b 2 という関係にあるなら、その三角形は直角三角形であるといえます。 そして、以下の2種類の直角三角形を覚える必要があります。 これらの角の大きさと辺の比をしっかり対応させましょう。 それぞれの辺の比は二等辺三角形・正三角形の性質から導けますが、
Incoming Term: 数学 三平方の定理 問題 難しい, 中3 数学 三平方の定理 問題, 中3 数学 三平方の定理 難問, 三平方の定理 問題 答え 付き, 三平方の定理 証明 中学生 簡単, 三平方の定理 計算 角度 底辺, 三平方の定理 30度 60度 90度, 三平方の定理 計算 30 60, 三平方の定理 30 60 90, 三平方の定理 証明 中学生 レポート,
コメント
コメントを投稿